
Procesamiento de señales digitales: señales DT básicas
AREAtutorial » Tutoriales de Ingeniería » Procesamiento de señales digitales: señales DT básicas
Hemos visto cómo las señales fundamentales se pueden representar en un dominio de tiempo continuo. Veamos cómo se pueden representar las señales fundamentales en el dominio del tiempo discreto.
Se denota como δ (n) en el dominio del tiempo discreto y se puede definir como;
$$ delta (n) = begin {cases} 1, & for quad n = 0 \ 0, & De lo contrario end {ases} $$

La señal discreta del paso de la unidad de tiempo se define como;
$$ U (n) = begin {cases} 1, & para quad n geq0 \ 0, & for quad n <0 end {cases} $$
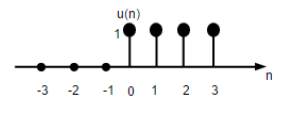
La figura anterior muestra una representación gráfica de una función de paso discreto.
La función de rampa de módulo discreto se puede definir como:
$$ r (n) = begin {cases} n, & para quad n geq0 \ 0, & for quad n <0 end {cases} $$
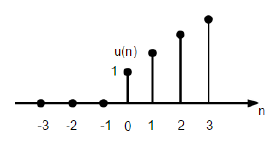
La figura anterior muestra una representación gráfica de una señal de línea discreta.
Una función parabólica de unidad discreta se denota como p (n) y se puede definir como;
$$ p (n) = begin {cases} \frac {n ^ {2}} {2}, & para quad n geq0 \ 0, & for quad n <0 end {cases} $$
En términos de la función de paso unitario, esto se puede escribir como;
$$ P (n) = \frac {n ^ {2}} {2} U (n) $$

La figura anterior muestra una representación gráfica de una secuencia parabólica.
Todas las señales de tiempo continuo son periódicas. Las secuencias sinusoidales de tiempo discreto pueden ser periódicas o no. Dependen del valor de ω. Para que una señal de tiempo discreto sea periódica, la frecuencia angular ω debe ser un múltiplo racional de 2π.
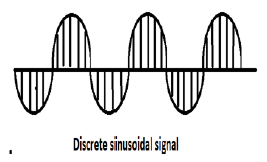
En la figura anterior se muestra una señal sinusoidal discreta.
La forma de onda sinusoidal discreta se puede representar en el formato:
$$ x (n) = A sin ( \omega n + phi) $$
Aquí A, ω y φ tienen sus significados habituales y n es un número entero. El período de tiempo de una señal sinusoidal discreta se define como:
$$ N = \frac {2 pi m} { omega} $$
Donde, N y m son números enteros.
🚫