
DSP – Operaciones de diferenciación de señales
AREAtutorial » Tutoriales de Ingeniería » DSP – Operaciones de diferenciación de señales
Dos operaciones muy importantes con señales son la diferenciación y la integración.
La diferenciación de cualquier señal x
$$ x
En el caso de la diferenciación OPAMP, esta metodología es muy útil. Podemos diferenciar fácilmente la señal gráficamente en lugar de usar una fórmula. Sin embargo, la condición es que la señal sea de tipo rectangular o triangular, que es el caso en la mayoría de los casos.
| Señal original | Señal diferenciada |
|---|---|
| Rampa | Paso |
| Paso | Legumbres |
| Legumbres | uno |
La tabla anterior muestra el estado de la señal después de la diferenciación. Por ejemplo, una señal lineal se convierte en una señal escalonada después de la diferenciación. Asimismo, una señal de un solo paso se convierte en una señal de pulso.
Démosle una señal $ x
Primero, comencemos a diferenciar esta ecuación. Sabemos que una señal lineal después de la diferenciación da una señal de un solo paso.
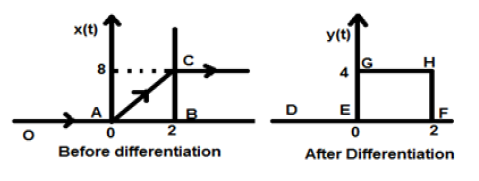
Por tanto, nuestra señal resultante y
$ y
$ = \frac {d4[r
$ = 4[u
Esta señal ahora se traza completamente, como se muestra en el lado derecho de la figura anterior.
🚫