
Comunicación analógica: moduladores AM
AREAtutorial » Tutoriales de Ingeniería » Comunicación analógica: moduladores AM
En este capítulo, analicemos los moduladores que generan una forma de onda modulada en amplitud. Los siguientes dos moduladores generan una onda AM.
A continuación se muestra un diagrama de bloques de un modulador de ley cuadrática.
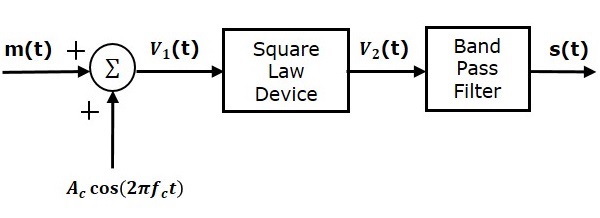
Deje que las señales de modulación y portadora se denoten como $ m \left (t \right) $ y $ A cos \left (2 pi f_ct \right) $, respectivamente. Estas dos señales se utilizan como entradas al sumador (sumador). Este bloque de verano genera una señal de salida, que es la suma de las señales de modulación y portadora. Matemáticamente, podemos escribir esto como
$$ V_1t = m \left (t \right) + A_c cos \left (2 pi f_ct \right) $$
Esta señal $ V_1t $ se envía a la entrada de un dispositivo no lineal como un diodo. Las características de un diodo están estrechamente relacionadas con la ley del cuadrado.
$ V_2t = k_1V_1 \left (t \right) + k_2V_1 ^ 2 \left (t \right) $ (Ecuación 1)
Donde $ k_1 $ y $ k_2 $ son constantes.
Sustituye $ V_1 \left (t \right) $ en la ecuación 1.
$$ V_2 \left (t \right) = k_1 left [ m\left ( t right ) + A_c cos \left ( 2 pi f_ct right ) right ] + k_2 left [ m\left ( t right ) + A_c cos\left ( 2 pi f_ct right ) right ]^ 2 $$
$ \Rightarrow V_2 \left (t \right) = k_1 m \left (t \right) + k_1 A_c cos \left (2 pi f_ct \right) + k_2 m ^ 2 \left (t \right) + $
$ k_2A_c ^ 2 cos ^ 2 \left (2 pi f_ct \right) + 2k_2m \left (t \right) A_c cos \left (2 pi f_ct \right) $
$ \Rightarrow V_2 \left (t \right) = k_1 m \left (t \right) + k_2 m ^ 2 \left (t \right) + k_2 A ^ 2_c cos ^ 2 \left (2 pi f_ct \right) + $
$ k_1A_c left [ 1+\left ( frac{2k_2}{k_1} right )m\left ( t right ) right ] cos \left (2 pi f_ct \right) $
El último término en la ecuación anterior representa la onda AM deseada, y los primeros tres términos en la ecuación anterior no son deseables. Entonces, con un filtro de paso de banda, podemos pasar solo la onda AM y eliminar los primeros tres términos.
Por lo tanto, la señal de salida del modulador cuadrático es
$$ s \left (t \right) = k_1A_c left [1+\left ( frac{2k_2}{k_1} right ) m\left ( t right ) right ] cos \left (2 pi f_ct \right) $$
Ecuación de onda AM estándar:
$$ s \left (t \right) = A_c left [ 1+k_am\left ( t right ) right ] cos \left (2 pi f_ct \right) $$
Donde, $ K_a $ – sensibilidad de amplitud
Comparando la salida del modulador cuadrático con la ecuación de onda AM estándar, obtenemos el factor de escala como $ k_1 $ y la sensibilidad de amplitud $ k_a $ como $ \frac {2k_2} {k1} $.
A continuación se muestra un diagrama de bloques del modulador de conmutación.
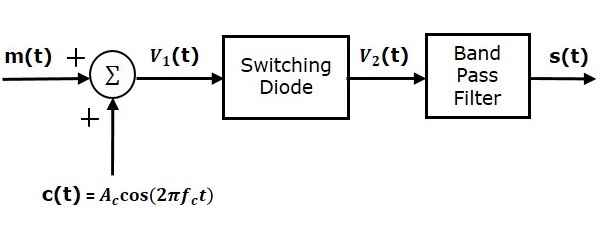
El modulador de conmutación es similar a los moduladores de ley cuadrada. La única diferencia es que en los moduladores de ley cuadrada, el diodo opera en un modo no lineal, mientras que en los moduladores de conmutación, el diodo debería funcionar como un interruptor ideal.
Deje que las señales de modulación y portadora se denoten como $ m \left (t \right) $ y $ c \left (t \right) = A_c cos \left (2 pi f_ct \right) $, respectivamente. Estas dos señales se utilizan como entradas para el sumador (sumador). El bloque Summer proporciona una señal de salida que es la suma de las señales portadora y de banda base. Matemáticamente, podemos escribir esto como
$$ V_1 \left (t \right) = m \left (t \right) + c \left (t \right) = m \left (t \right) + A_c cos \left (2 pi f_ct right ) $$
Esta señal $ V_1 \left (t \right) $ se aplica como entrada al diodo. Supongamos que la magnitud de la señal moduladora es muy pequeña en comparación con la amplitud de la señal portadora $ A_c $. Por lo tanto, el encendido y apagado del diodo está controlado por la señal portadora $ c \left (t \right) $. Esto significa que el diodo estará polarizado hacia adelante cuando $ c \left (t \right)> 0 $, y estará polarizado hacia atrás cuando $ c \left (t \right)
Por lo tanto, a la salida del diodo
$$ V_2 \left (t \right) = left { begin {matrix} V_1 \left (t \right) & if & c \left (t \right)> 0 \ 0 & if & c \left (t cierto)
Podemos aproximar esto como
$ V_2 \left (t \right) = V_1 \left (t \right) x \left (t \right) $ (Ecuación 2)
Donde $ x \left (t \right) $ es una secuencia periódica de pulsos con un período de tiempo $ T = \frac {1} {f_c} $

Este tren de pulsos periódico se representa como una serie de Fourier:
$$ x \left (t \right) = \frac {1} {2} + \frac {2} { pi} sum_ {n = 1} ^ { infty} \frac { \left (-1 \right) ^ n-1} {2n-1} cos \left (2 pi \left (2n-1 \right) f_ct \right) $$
$$ \Rightarrow x \left (t \right) = \frac {1} {2} + \frac {2} { pi} cos \left (2 pi f_ct \right) – \frac {2} { 3 pi} cos \left (6 pi f_ct \right) +…. $$
Sustituye los valores $ V_1 \left (t \right) $ y $ x \left (t \right) $ en la ecuación 2.
$ V_2 \left (t \right) = left [ m\left ( t right )+A_c cos\left ( 2 pi f_ct right ) right ] izquierda [ frac{1}{2} + frac{2}{pi} cos \left ( 2 pi f_ct right )-frac{2}{3pi} cos\left ( 6 pi f_ct right )+…..right ]PS
$ V_2 \left (t \right) = \frac {m \left (t \right)} {2} + \frac {A_c} {2} cos \left (2 pi f_ct \right) + \frac { 2m \left (t \right)} { pi} cos \left (2 pi f_ct \right) + \frac {2A_c} { pi} cos ^ 2 \left (2 pi f_ct \right) – PS
$ \frac {2m \left (t \right)} {3 pi} cos \left (6 pi f_ct \right) – \frac {2A_c} {3 pi} cos \left (2 pi f_ct \right) cos \left (6 pi f_ct \right) +….. $
$ V_2 \left (t \right) = \frac {A_c} {2} \left (1+ \left ( \frac {4} { pi A_c} \right) m \left (t \right) \right) cos \left (2 pi f_ct \right) + \frac {m \left (t \right)} {2} + \frac {2A_c} { pi} cos ^ 2 \left (2 pi f_ct \right) – $
$ \frac {2m \left (t \right)} {3 pi} cos \left (6 pi f_ct \right) – \frac {2A_c} {3 pi} cos \left (2 pi f_ct \right) cos \left (6 pi f_ct \right) +….. $
El primer término de la ecuación anterior representa la onda AM deseada y los términos restantes no son deseados. Por lo tanto, con la ayuda de un filtro de paso de banda, podemos pasar solo la onda AM y excluir el resto de los términos.
Por lo tanto, la salida del modulador de conmutación es
$$ s \left (t \right) = \frac {A_c} {2} \left (1+ \left ( \frac {4} { pi A_c} \right) m \left (t \right) right ) cos \left (2 pi f_ct \right) $$
Sabemos que la ecuación de onda de AM estándar es:
$$ s \left (t \right) = A_c left [ 1+k_am\left ( t right ) right ] cos \left (2 pi f_ct \right) $$
Donde $ k_a $ es la sensibilidad de amplitud.
Comparando la salida del modulador de conmutación con la ecuación de forma de onda AM estándar, obtenemos un factor de escala de 0.5 y una sensibilidad de amplitud $ k_a $ como $ \frac {4} { pi A_c} $.
🚫