
Comunicación analógica: modulación VSBSC
AREAtutorial » Tutoriales de Ingeniería » Comunicación analógica: modulación VSBSC
En los capítulos anteriores, discutimos la modulación y demodulación SSBSC. La señal SSBSC modulada tiene solo una frecuencia de banda lateral. En teoría, podemos obtener un componente de frecuencia de banda lateral completo utilizando un filtro de paso de banda ideal. Sin embargo, en la práctica no podemos obtener el componente de frecuencia completo de la banda lateral. Debido a esto, se pierde parte de la información.
Para evitar esta pérdida, se elige un método que sea un compromiso entre DSBSC y SSBSC. Este método se conoce como Portadora remanente suprimida de banda lateral (VSBSC) equipo. La palabra «remanente» significa «parte» de la que proviene el nombre.
Modulación VSBSC es un proceso en el que una parte de la señal, llamada traza, se modula junto con una banda lateral. El espectro de frecuencia de la onda VSBSC se muestra en la siguiente figura.
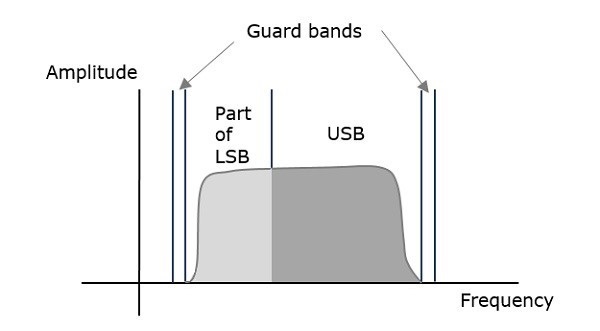
Junto con la banda lateral superior, este método transfiere parte de la banda lateral inferior. Asimismo, podemos transferir la franja lateral inferior junto con parte de la franja lateral superior. Se ha colocado una tira de protección muy pequeña a cada lado del VSB para evitar interferencias. La modulación VSB se utiliza principalmente en transmisiones de televisión.
Sabemos que el ancho de banda de la forma de onda modulada SSBSC es $ f_m $. Dado que la onda modulada VSBSC contiene los componentes de frecuencia de una banda lateral junto con el resto de la otra banda lateral, su ancho de banda será la suma del ancho de banda modulado SSBSC y la frecuencia residual $ f_v $.
aquellos. Ancho de banda modulado VSBSC = $ f_m + f_v $
A continuación se muestran los beneficios de la modulación VSBSC.
Muy eficiente.
Ancho de banda reducido en comparación con las ondas AM y DSBSC.
El diseño del filtro es simple ya que no se requiere alta precisión.
La transmisión de componentes de baja frecuencia es posible sin ninguna dificultad.
Tiene buenas características de fase.
Las siguientes son las desventajas de la modulación VSBSC.
El ancho de banda es mayor en comparación con la onda SSBSC.
La demodulación es complicada.
La aplicación más famosa y estándar de las VSBSC es la transmisión de señales de televisión. También es el método más conveniente y eficiente en términos de uso de ancho de banda.
Ahora analicemos el modulador que genera las ondas VSBSC y el demodulador que demodula las ondas VSBSC una por una.
Generar una onda VSBSC es similar a generar una onda SSBSC. El modulador VSBSC se muestra en la siguiente figura.
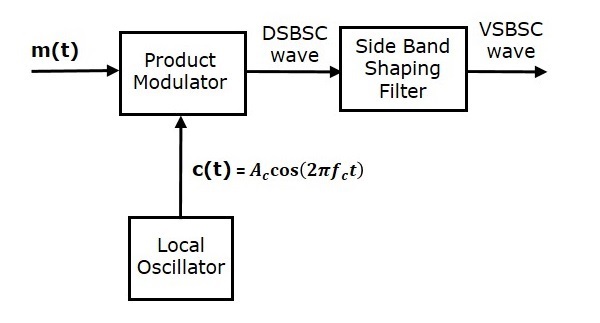
En este método, primero generaremos una onda DSBSC usando un modulador de producto. Luego aplique esta onda DSBSC como entrada al filtro de conformación de banda lateral. Este filtro produce una señal de salida que es una onda VSBSC.
La señal de modulación $ m \left (t \right) $ y la señal portadora $ A_c cos \left (2 pi f_ct \right) $ se utilizan como entradas al modulador de producto. En consecuencia, el modulador de producto produce una salida que es el producto de estas dos entradas.
Por lo tanto, la salida del modulador de producto es
$$ p \left (t \right) = A_c cos \left (2 pi f_ct \right) m \left (t \right) $$
Aplicar la transformada de Fourier en ambos lados
$$ P \left (f \right) = \frac {A_c} {2} left [ M\left ( f-f_c right )+M\left ( f+f_c right ) right ]$$
La ecuación anterior es una ecuación de espectro de frecuencia DSBSC.
Sea la función de transferencia del filtro de conformación de banda lateral $ H \left (f \right) $. Este filtro tiene una entrada $ p \left (t \right) $ y una salida es una onda modulada VSBSC $ s \left (t \right) $. Las transformadas de Fourier para $ p \left (t \right) $ y $ s \left (t \right) $ son $ P \left (t \right) $ y $ S \left (t \right) $, respectivamente.
Matemáticamente, podemos escribir $ S \left (f \right) $ como
$$ S \left (t \right) = P \left (f \right) H \left (f \right) $$
Sustituye el valor $ P \left (f \right) $ en la ecuación anterior.
$$ S \left (f \right) = \frac {A_c} {2} left [ M\left ( f-f_c right )+M\left ( f+f_c right ) right ]H \left (f \right) $$
La ecuación anterior es la ecuación del espectro de frecuencia VSBSC.
La demodulación de la onda VSBSC es similar a la demodulación de la onda SSBSC. Aquí, la misma señal portadora (que se usa para generar la onda VSBSC) se usa para detectar la señal del mensaje. Por lo tanto, este proceso de descubrimiento se llama consistente o detección sincrónica… El demodulador VSBSC se muestra en la siguiente figura.
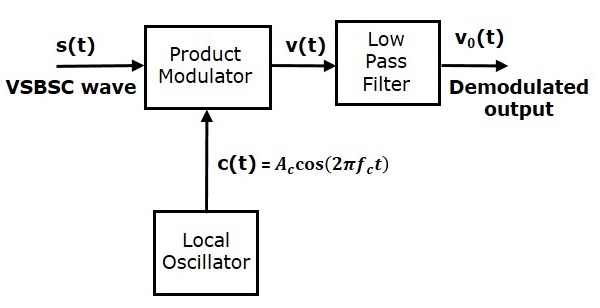
En este proceso, la señal del mensaje se puede extraer de la onda VSBSC multiplicándola por una portadora que tiene la misma frecuencia y fase de la portadora que se utiliza en la modulación VSBSC. La señal resultante luego pasa a través de un filtro de paso bajo. La salida de este filtro es la señal del mensaje deseado.
Sea la onda VSBSC $ s \left (t \right) $ y la señal portadora $ A_c cos \left (2 pi f_ct \right) $.
En la figura, podemos escribir la señal de salida del modulador de producto como
$$ v \left (t \right) = A_c cos \left (2 pi f_ct \right) s \left (t \right) $$
Aplicar la transformada de Fourier en ambos lados
$$ V \left (f \right) = \frac {A_c} {2} left [ S\left ( f-f_c right )+S\left ( f+f_c right ) right ]$$
Sabemos que $ S \left (f \right) = \frac {A_c} {2} left [ M\left ( f-f_c right ) + M\left ( f+f_c right )right ]H \left (e \right) $
De la ecuación anterior, encuentre $ S \left (f-f_c \right) $ y $ S \left (f + f_c \right) $.
$$ S \left (f-f_c \right) = \frac {A_c} {2} left [ M\left ( f-f_c-f_c right ) + M\left ( f-f_c+f_c right )right ]H \left (f-f_c \right) $$
$ \Rightarrow S \left (f-f_c \right) = \frac {A_c} {2} left [ M\left ( f-2f_c right )+M\left ( f right ) right ] H \left (f-f_c \right) $
$$ S \left (f + f_c \right) = \frac {A_c} {2} left [ M\left ( f+f_c-f_c right ) +M\left ( f+f_c+f_c right )right ] H \left (f + f_c \right) $$
$ \Rightarrow S \left (f + f_c \right) = \frac {A_c} {2} left [ M \left ( f right )+M \left (f+2f_c right ) right ] H \left (f + f_c \right) $
Reemplaza los valores $ S \left (f-f_c \right) $ y $ S \left (f + f_c \right) $ en $ V \left (f \right) $.
$ V (f) = \frac {A_c} {2}[frac{A_c}{2}[M(f-2f_c)+M(f)]H (f-f_c) + $
$ \frac {A_c} {2}[M(f)+M(f+2f_c)]H (f + f_c)]$
$ \Rightarrow V \left (f \right) = \frac {{A_ {c}} ^ {2}} {4} M \left (f \right) left [ H\left ( f-f_c right )+H \left ( f+f_c right ) right ]PS
$ + \frac {{A_ {c}} ^ {2}} {4} left [ M\left ( f-2f_c right )H\left ( f-f_c right )+M\left ( f+2f_c right )H\left ( f+f_c right ) right ]PS
En la ecuación anterior, el primer término representa una versión escalada del espectro de frecuencias de la señal de mensaje deseada. Se puede extraer pasando la señal anterior a través de un filtro de paso bajo.
$$ V_0 \left (f \right) = \frac {{A_ {c}} ^ {2}} {4} M \left (f \right) left [ H\left ( f-f_c right )+H\left ( f+f_c right ) right ]$$
🚫