
Teoría de la antena – vector de Poynting
AREAtutorial » Tutoriales de Ingeniería » Teoría de la antena – vector de Poynting
Las antenas emiten energía electromagnética para transmitir o recibir información. Por tanto, las condiciones Energía y Poder están asociadas con estas ondas electromagnéticas y debemos discutirlas. Una onda electromagnética tiene campos eléctricos y magnéticos.
Considere una onda en cualquier momento que se pueda ver en ambos vectores. La siguiente figura muestra una representación de los componentes del campo eléctrico y magnético en una onda electromagnética.
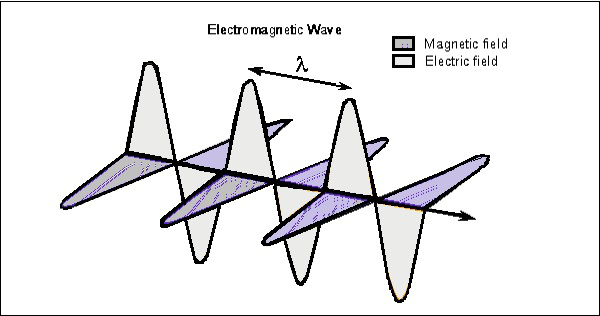
La onda eléctrica está presente verticalmente con respecto a la propagación de la onda electromagnética, mientras que la onda magnética es horizontal. Ambos campos forman ángulos rectos entre sí.
El vector de Poynting describe la energía de una onda electromagnética por unidad de tiempo por unidad de área en un momento dado. John Henry Poynting recibió este vector por primera vez en 1884 y, por lo tanto, recibió su nombre.
Definición – «El vector de Poynting da la tasa de transferencia de energía por unidad de área»
o
«La energía que transporta una onda por unidad de tiempo por unidad de área viene dada por el vector de Poynting».
El vector de Poynting se representa como S…
La unidad SI del vector de Poynting es W / m2…
La cantidad que se usa para describir la potencia asociada con las ondas electromagnéticas es la cantidad instantánea. Vector de poyntingque se define como
$$ hat {S} = hat {E} times hat {H} $$
Dónde
$ hat {S} $ – Vector instantáneo de Poynting. (W / m2)…
$ hat {E} $ – intensidad de campo eléctrico instantáneo. (W / m)…
$ hat {H} $ – intensidad del campo magnético instantáneo. (Estoy)…
Es importante señalar aquí que el valor de E es mayor que H dentro de la onda electromagnética. Sin embargo, ambos aportan la misma cantidad de energía. Ŝ es un vector que tiene dirección y magnitud. La dirección Ŝ coincide con la velocidad de la onda. Su valor depende de E y H.
Para tener una comprensión clara del vector de Poynting, analicemos la derivación de este vector de Poynting en un proceso paso a paso.
Imagine que una onda electromagnética pasa por la región (A), perpendicular al eje X, a lo largo de la cual se propaga la onda. Al pasar por A en un tiempo infinitesimal (dt), la onda recorre la distancia (dx).
$$ dx = C dt $$
Dónde
$$ C = velocidad light = 3 times 10 ^ {8} m / s $$ $$ volumen, dv = Adx = AC dt $$ $$ d mu = mu dv = ( epsilon_ {0 } E ^ {2}) (AC dt) $$ $$ = epsilon_ {0} AC E ^ {2} dt $$
Por lo tanto, la energía transferida en el tiempo (dt) al área (A) es –
$$ S = \frac {Energía} {Tiempo tiempos Área} = \frac {dW} {dt A} = \frac { epsilon_ {0} ACE ^ {2} dt} {dt A} = épsilon_ {0} C : E ^ {2} $$
DESDE
$$ \frac {E} {H} = sqrt { \frac { mu_ {0}} { epsilon_ {0}}} luego S = \frac {CB ^ {2}} { mu_ {0 }} $$
DESDE
$$ C = \frac {E} {H} entonces S = \frac {EB} { mu_ {0}} $$ $$ = hat {S} = \frac {1} { mu_ {0 }} ( hat {E} hat {H}) $$
S denota el vector de Poynting.
La ecuación anterior nos da energía por unidad de tiempo por unidad de área en un momento dado, que se llama Vector de poynting…
🚫