Python – datos gráficos

Python – gráfico de datos

CSGraph significa Gráfico disperso comprimido, que se centra en algoritmos de gráficos rápidos basados ​​en representaciones matriciales dispersas.

Representaciones gráficas

Primero, entendamos qué es un gráfico disperso y cómo ayuda con las representaciones de gráficos.

¿Qué es un gráfico disperso?

Un gráfico es simplemente una colección de nodos que tienen conexiones entre ellos. Los gráficos pueden representar casi todo: conexiones en redes sociales, donde cada nodo es una persona y está conectado con conocidos; imágenes, donde cada nodo es un píxel y está asociado con píxeles vecinos; puntos en una distribución multivariante, donde cada nodo está relacionado con sus vecinos más cercanos y casi todo lo demás que puedas imaginar.

Una forma muy eficiente de representar los datos de un gráfico es una matriz dispersa: llamémosla G. La matriz G es N x N y G[i, j] da el valor de la conexión entre el nodo «i» y el nodo «j». Un gráfico disperso contiene principalmente ceros, es decir, la mayoría de los nodos tienen solo unas pocas conexiones. Esta propiedad resulta ser cierta en los casos más interesantes.

La creación de un submódulo de gráfico disperso fue motivada por varios algoritmos utilizados en scikit-learn, que incluían lo siguiente:

• Isomap – Un algoritmo para el aprendizaje de la diversidad, que requiere encontrar los caminos más cortos en un gráfico.

• Agrupación jerárquica – Un algoritmo de agrupamiento basado en un árbol de expansión mínimo.

• Descomposición espectral – Un algoritmo de proyección basado en el laplaciano de gráficos dispersos.

Como ejemplo específico, imagine que nos gustaría presentar el siguiente gráfico no dirigido:

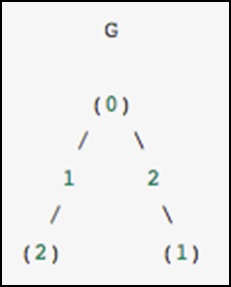
Este gráfico tiene tres nodos, donde el nodo 0 y 1 están conectados por un borde de peso 2, y los nodos 0 y 2 están conectados por un borde de peso 1. Podemos construir representaciones densas, enmascaradas y dispersas, como se muestra a continuación. ejemplo., teniendo en cuenta que un gráfico no dirigido está representado por una matriz simétrica.

G_dense = np.array([ [0, 2, 1],
                     [2, 0, 0],
                     [1, 0, 0] ])
                     
G_masked = np.ma.masked_values(G_dense, 0)
from scipy.sparse import csr_matrix

G_sparse = csr_matrix(G_dense)
print G_sparse.data

El programa anterior generará la siguiente salida.

array([2, 1, 2, 1])

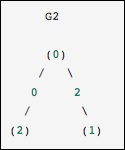
Esto es idéntico al gráfico anterior, excepto que los nodos 0 y 2 están conectados por un borde con peso cero. En este caso, la representación densa anterior conduce a la ambigüedad: ¿cómo se pueden representar los no bordes si cero es un valor significativo? En este caso, se debe utilizar una representación enmascarada o dispersa para eliminar la ambigüedad.

Considere el siguiente ejemplo.

from scipy.sparse.csgraph import csgraph_from_dense
G2_data = np.array
([
   [np.inf, 2, 0 ],
   [2, np.inf, np.inf],
   [0, np.inf, np.inf]
])
G2_sparse = csgraph_from_dense(G2_data, null_value=np.inf)
print G2_sparse.data

El programa anterior generará la siguiente salida.

array([ 2., 0., 2., 0.])