
Matemáticas discretas – relaciones
AREAtutorial » Tutoriales de Ingeniería » Matemáticas discretas – relaciones
Siempre que se discuten los conjuntos, lo siguiente que viene a la mente es la relación entre los elementos de los conjuntos. conexiones Puede existir entre objetos del mismo conjunto o entre objetos de dos o más conjuntos.
La relación binaria R de un conjunto xay (escrito como $ xRy $ o $ R (x, y) $) es un subconjunto del producto cartesiano $ x times y $. Si se invierte el par ordenado G, la relación también cambia.
Por lo general, la relación n-aria R entre los conjuntos $ A_1, dots, y A_n $ es un subconjunto del producto n-ario $ A_1 times dots times A_n $. La cardinalidad mínima de la razón R es cero, y el máximo en este caso es $ n ^ 2 $.
Una relación binaria R en un conjunto A es un subconjunto de $ A times A $.
Para dos conjuntos diferentes A y B con potencias metro y PAG en consecuencia, la cardinalidad máxima de la relación R de A a B es millón…
Si hay dos conjuntos A y B, y la relación R tiene un par de órdenes (x, y), entonces –
EN dominio R, Dom (R), es el conjunto $ lbrace x : | : (x, y) en R : para : algunos : y : en : B rbrace $
EN clasificar R, Ran (R), es el conjunto $ lbrace y : | : (x, y) en R : para : algunos : x : en : A rbrace $
Sea $ A = lbrace 1, 2, 9 rbrace $ y $ B = lbrace 1, 3, 7 rbrace $
Caso 1 – Si R ‘es igual a’ entonces $ R = lbrace (1, 1), (3, 3) rbrace $
Dom (R) = $ lbrace 1, 3 rbrace, Ran (R) = lbrace 1, 3 rbrace $
Caso 2 – Si R ‘es menor que’ entonces $ R = lbrace (1, 3), (1, 7), (2, 3), (2, 7) rbrace $
Dom (R) = $ lbrace 1, 2 rbrace, Ran (R) = lbrace 3, 7 rbrace $
Caso 3 – Si R ‘es mayor que’ entonces $ R = lbrace (2, 1), (9, 1), (9, 3), (9, 7) rbrace $
Dom (R) = $ lbrace 2, 9 rbrace, Ran (R) = lbrace 1, 3, 7 rbrace $
La relación se puede representar mediante un gráfico dirigido.
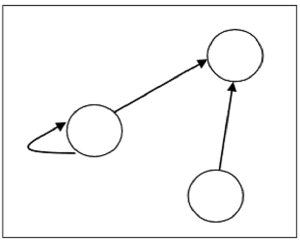
El número de vértices del gráfico es igual al número de elementos del conjunto a partir del cual se determinó la relación. Para cada par ordenado (x, y) en relación R, habrá una arista dirigida desde el vértice x al vértice y. Si hay un par ordenado (x, x), habrá un bucle en el vértice x.
Supongamos que hay una relación $ R = lbrace (1, 1), (1,2), (3, 2) rbrace $ en el conjunto $ S = lbrace 1, 2, 3 rbrace $, puede ser representado siguiente gráfico –
EN Relación vacía entre los conjuntos X e Y, o en E, hay un conjunto vacío $ emptyset $
EN Actitud plena entre los conjuntos X e Y hay un conjunto $ X times Y $
EN Relación de identidad el conjunto X contiene el conjunto $ lbrace (x, x) | x in X rbrace $
La relación inversa R ‘de la relación R se define como – $ R’ = lbrace (b, a) | (a, b) in R rbrace $
Ejemplo – Si $ R = lbrace (1, 2), (2, 3) rbrace $, entonces $ R ‘$ será $ lbrace (2, 1), (3, 2) rbrace $
Una relación R en un conjunto A se llama reflexivo si $ forall a in A $ está asociado con a (se ejecuta aRa)
Ejemplo – La relación $ R = lbrace (a, a), (b, b) rbrace $ en el conjunto $ X = lbrace a, b rbrace $ es reflexiva.
Una relación R en un conjunto A se llama No reflectante si no hay $ a en A $ asociado con a (aRa no se satisface).
Ejemplo – La relación $ R = lbrace (a, b), (b, a) rbrace $ en el conjunto $ X = lbrace a, b rbrace $ es irreflexiva.
Una relación R en un conjunto A se llama Simétrico si $ yRx $, $ forall x en A $ y $ forall y en A $ se sigue de $ xRy $.
Ejemplo – La relación $ R = lbrace (1, 2), (2, 1), (3, 2), (2, 3) rbrace $ en el conjunto $ A = lbrace 1, 2, 3 rbrace $ es igual a simétrico…
Una relación R en un conjunto A se llama Antisimétrico si $ x = y : forall x en A $ y $ forall y en A $ se sigue de $ xRy $ y $ yRx $.
Ejemplo – La razón de $ R = lbrace (x, y) a N | : x leq y rbrace $ es antisimétrico porque $ x leq y $ y $ y leq x $ implican $ x = y $.
Una relación R en un conjunto A se llama Transición si $ xRz, forall x, y, z en A $ se sigue de $ xRy $ y $ yRz $.
Ejemplo – La relación $ R = lbrace (1, 2), (2, 3), (1, 3) rbrace $ en el conjunto $ A = lbrace 1, 2, 3 rbrace $ es transitiva.
La actitud es Relación de equivalencia si es reflexiva, simétrica y transitiva.
Ejemplo – Razón $ R = lbrace (1, 1), (2, 2), (3, 3), (1, 2), (2,1), (2,3), (3,2), ( 1,3), (3,1) rbrace $ en el conjunto $ A = lbrace 1, 2, 3 rbrace $ es una relación de equivalencia, ya que es reflexiva, simétrica y transitiva.
🚫